Tranquilos, no voy a hablar ni de blockchain ni de geoposicionamiento, sino de un tema más aburrido y básico: sobre funciones hash y hash maps.
En este post os contaré un caso real en Nextail, donde el cambio de una sóla línea de código relacionada con una función hash cambió el rendimiento de una aplicación, tanto por consumo de CPU como de memoria.
David me sugirió titular el post con “Cómo ahorrar miles de euros a tu empresa cambiando una línea de código”, pero como no he sido capaz de cuantificarlo objetivamente he optado por un título con menos clickbait.
Las funciones hash son una herramienta básica en tecnología, con múltiples aplicaciones prácticas. Es importante conocer su funcionamiento y las implicaciones que puede tener elegir mal una función hash.
El problema
En Nextail manejamos un gran volumen de datos, pero el dominio básico sobre el que aplican los mismos se puede decir que es limitado: países, ciudades, tiendas, productos, referencias de productos, etc. De media en un cliente, el número de países, ciudades o tiendas no suele superar el orden de millares, y el de referencias de productos los centenares de millares.
Si al guardar todas esas entidades en base de datos utilizas una clave primaria generada mediante una secuencia, te encuentras con que los identificadores son números enteros que van de 1 a N, siendo N un número relativamente bajo comparado con el rango de los enteros positivos de 32 bits (de 0 a 2.147.483.647).
En la lógica de negocio es muy normal a la hora de trabajar con esa información que necesites usar datos relacionados con dos entidades de tu dominio, por ejemplo, el stock o las ventas de un producto en una determinada tienda.
En base de datos esa información puede estar guardada en una tabla, y para localizar rápidamente datos de un producto en una tienda crearíamos un índice compuesto por los identificadores de la tienda y del producto. Cuando en tu lógica de negocio tienes toda esa información en memoria en forma de objetos, para poder trabajar sobre todos ellos lo normal será que esos objetos acaben en un mapa o diccionario.
El uso de ésta estructura de datos se convierte en crítico por el número de operaciones que acaban usándola. Una mala elección de la función hash a aplicar en esta estructura de datos puede llegar a penalizar el consumo de memoria y el rendimiento de tu aplicación.
Para entender el problema de estos índices compuestos en un mapa haremos primero un repaso de la estructura de datos.
El código fuente con los ejemplos y las utilidades para realizar métricas lo puedes encontrar en este repositorio de github
Mapa
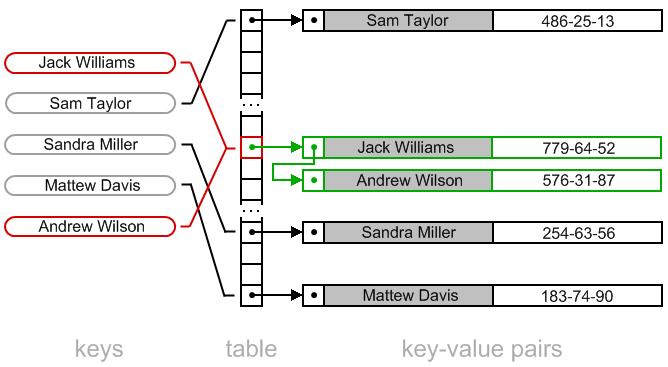
La forma más eficiente de implementar un mapa es mediante tablas hash, y un punto importante para que una tabla hash funcione bien es la función de hash que aplicará sobre su clave.
En Java la implementación que más se usa es HashMap (no uséis HashTable, uno de los errores de juventud de Java). Si el orden en el que poder recorrer las claves es importante puedes usar un TreeMap, pero si la concurrencia te preocupa deberías usar un ConcurrentHashMap.
En cualquiera de los casos, Java sólo le pide dos cosas al objeto que uses como clave en el mapa:
- Que reimplemente el método hashCode() que hereda de la clase Object: si no lo reimplementa, usará algo que va en función de la dirección de memoria de la instancia. Por tanto, dos instancias idénticas en datos tendrán valores distintos de
hashCode. - Que reimplemente el método equals() que hereda de la clase Object: si no lo reimplementa comparará las referencias de las instancias, por lo que pasará también que instancias idénticas en datos no las considerará iguales.
Por tanto, si no reimplementas ninguno de los dos métodos estarás introduciendo bugs en tu aplicación. ¿Cuál es el valor que sale por consola al ejecutar el siguiente código? ¿Cuál sería el valor esperado?
public class Person {
private Integer id;
private String name;
public Person(Integer id, String name) {
this.id = id;
this.name = name;
}
}
public static void main(String[] args) {
Map<Person, Integer> map = new HashMap<>();
map.put(new Person(1, "Alberto"), 35);
map.put(new Person(2, "Ana"), 28);
//más operaciones y en un lugar alejado del código...
map.put(new Person(1, "Alberto"), 36);
System.out.println(map.size());
}
El resultado esperado es que hubiera 2 objetos en el mapa, pero nos encontramos 3, ya que la segunda vez que añadimos a Alberto con id = 1, no considerará que ya existe y creará otra entrada en el mapa.
Cómo implementar las funciones hashCode y equals dependerá de tu lógica de negocio, y de cómo definas la identidad de tu objeto, pero deberías usar los mismos atributos que definirían tu clave primaria si estuviera en base de datos.
Con la ayuda de nuestro IDE favorito podemos generar fácilmente todo este código verboso, pero necesario:
public class Person {
private Integer id;
private String name;
public Person(Integer id, String name) {
this.id = id;
this.name = name;
}
public int hashCode() {
return Objects.hash(id);
}
public boolean equals(Object obj) {
if (this == obj)
return true;
if (obj == null)
return false;
if (getClass() != obj.getClass())
return false;
Person other = (Person) obj;
return Objects.equals(id, other.id);
}
}
Os invito a realizar la misma prueba en JavaScript, el resultado os sorprenderá, o no… :)
La función hash
Para este ejemplo he dejado como función hash el código que me autogenera el IDE, que hace uso de la versión propuesta por Java. Aunque hubiera sido incluso mejor y más sencillo haber devuelto el valor de id directamente.
El método llama a este código sobre la clase Arrays, que es el estándar para calcular el hash de una clave compuesta:
public static int hashCode(Object a[]) {
if (a == null) return 0;
int result = 1;
for (Object element : a)
result = 31 * result + (element == null ? 0 : element.hashCode());
return result;
}
Para buscar la mayor dispersión de las claves, itera los elementos que forman la clave multiplicando por 31 el anterior valor y sumando el hashCode del valor iterado.
Para entender las razones de elegir ese 31, mejor citar a Joshua Bloch en su imprescindible libro de Effective Java:
The value 31 was chosen because it is an odd prime. If it were even and the multiplication overflowed, information would be lost, as multiplication by 2 is equivalent to shifting. The advantage of using a prime is less clear, but it is traditional. A nice property of 31 is that the multiplication can be replaced by a shift and a subtraction for better performance: 31 * i == (i « 5) - i. Modern VMs do this sort of optimization automatically.
Que ésta sea la función hash propuesta como por defecto en Java no significa que sea la mejor en todas las circunstancias. En la mayoría de los casos da unos resultados satisfactorios y cumple con los requisitos que se le piden a una función hash, pero en algunos casos deberemos replantearnos su idoneidad.
Colisiones
Una de las propiedades más importantes de una función hash es que el resultado sea uniforme:
Se dice que una función resumen es uniforme cuando para una clave elegida aleatoriamente es igualmente probable tener un valor resumen determinado, independientemente de cualquier otro elemento.
De esta forma se minimiza el número de valores coincidentes y que la implementación del hash table tenga que trabajar menos en reubicar los valores coincidentes en su hash.
Cómo resolver esto es una de las partes donde más esfuerzo hacen las distintas implementaciones de hash table y que da para muchos papers. Dependiendo de cómo sea esa distribución de las colisiones (por tanto tu función hash), una implementación de hash table puede pasar de tener coste de O(1) a uno de O(n) para las operaciones de inserción y consulta.
Análisis de la función hash estándar de Java
Volviendo a lo que os contaba al principio, ¿Qué pasa cuando analizamos el comportamiento de la función hash facilitada por Java sobre objetos con las siguientes características?
- Son objetos que guardan información sobre dos entidades relacionadas, y por tanto su clave (y la función hash) está formada por dos valores.
- Las claves son un subconjunto de los valores enteros, que van de 0 a N, siendo N un valor relativamente bajo.
Un objeto que lo represente puede tener esta forma:
public class MyObject {
private MyObjectKey key;
private String someAttribute;
public MyObject(int firstKey, int secondKey, String someAttribute) {
this.key = new MyObjectKey(firstKey, secondKey);
this.someAttribute = someAttribute;
}
public MyObjectKey getKey() { return key; }
public String getSomeAttribute() { return someAttribute; }
public int hashCode() { return key.hashCode(); }
public boolean equals(Object obj) { ... }
}
public class MyObjectKey {
private int firstKey;
private int secondKey;
public MyObjectKey(int firstKey, int secondKey) {
this.firstKey = firstKey;
this.secondKey = secondKey;
}
public int getFirstKey() { return firstKey; }
public int getSecondKey() { return secondKey; }
public int hashCode() {
int result = 31 + firstKey;
return 31 * result + secondKey;
}
public boolean equals(Object obj) { ... }
}
Un uso simplificado de esta clase con un Map en Java podría ser:
Map<MyObjectKey, MyObject> map = new HashMap<>();
//Or loaded from database:
MyObject obj1 = new MyObject(1311, 313, "Madrid");
MyObject obj2 = new MyObject(1332, 313, "Barcelona");
MyObject obj3 = new MyObject(1311, 928, "Zaragoza");
....
....
map.put(obj1.getKey(), obj1);
map.put(obj2.getKey(), obj2);
map.put(obj3.getKey(), obj3);
Si miramos las tripas de la clase Map vemos que no usa el valor que devuelve tu función hash directamente, sino que aplica una transformación más para mejorar la dispersión de la función:
static final int hash(Object key) {
int h;
return (key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16);
}
¿Qué pasa si cargamos en memoria todos los objetos cuya clave cubra los siguientes valores?
- firstKey: de 0 a 50.000, que podrían representar los identificadores de mis productos
- secondKey: de 0 a 1.000, que podrían representar los identificadores de las tiendas
Estamos cargando 50 millones de objetos en el caso pesimista de que todos los productos estuvieran en todas la tiendas.
Si analizamos el número de colisiones con un código que reproduce los cálculos y colisiones de cargar todos esos registros en un HashMap:
for (int i = 0; i < n_products; i++) {
for (int j = 0; j < n_stores; j++) {
int hashValue = HashMap.hash(Objects.hash(i, j));
histogram.add(hashValue);
}
}
Vemos que pasa lo siguiente:
- 399.744 veces sucede que 33 instancias colisionan entre sí
- 1.149.303 veces sucede que 32 instancias colisionan entre sí.
- 62 veces sucede que 31 instancias colisionan entre sí
- 62 veces sucede que 30 instancias colisionan entre sí
- 62 veces sucede que i< 30 instancias colisionan entre sí hasta i=1
Es decir, el 99,93% de las veces cualquier combinación de un producto y una tienda colisionará con al menos otros 31 valores.
¿Qué consecuencias tiene esto?
- Deja de comportarse como un HashMap y se parece más a un árbol
- La estructura en árbol consume más memoria
- Hace un uso intensivo de la función
equalsde la clave
En resumen: hay un gran consumo de memoria y de CPU.
¿Cómo resuelve HashMap las colisiones?
Internamente HashMap define un array de nodos de cierto tamaño que va variando según el número total de elementos. Del valor resultante de aplicar la función hash se queda con el resto de su división con el tamaño actual de ese array.
Por tanto, no sólo hay que tener en cuenta el número de colisiones de la función hash, sino que hay que tener además en cuenta el número de colisiones al dividir por el tamaño de ese array y quedarse con el resto.
Si dos claves resulta que tienen el mismo resultado al aplicar la función hash, acabarán en la misma posición del array. HashMap utiliza la técnica de direccionamiento cerrado con hashing abierto: cada elemento del array contiene una lista enlazada de nodos donde va concatenando al final de la misma, según van llegando colisiones en esa posición del array.
Cada uno de los nodos de la lista contiene: la clave, el valor, el hash de la clave y la referencia al siguiente elemento de la lista.
Si la función hash es suficientemente buena, el número de elementos en las listas será bajo, y el número de encadenamientos será también bajo. Pero si tenemos la mala suerte de que haya muchas colisiones, la implementación de HashMap cambia de estrategia y en vez de gestionar una lista enlazada de complejidad O(n), cambia a un árbol rojo-negro con complejidad O(log n).
Este comportamiento fue introducido en Java 8 para mejorar el rendimiento de forma transparente para los desarrolladores y manteniendo la compatibilidad hacía atrás, como nos tienen acostumbrados.
En HashMap, el número necesario de colisiones en una misma posición del array para que pase a ser un árbol es de 8. Si volvemos a mi ejemplo, ese valor se alcanza en el 99.99% de los casos, por lo que siempre que necesitemos acceder al mapa, tendremos además que recorrer un árbol.
Consumo de memoria
Al tener que cambiar a una estructura de árbol en el 99.99% de los nodos, el consumo de memoria aumenta. El elemento del array pasa a ser un TreeNode, que extiende de la clase Node y le añade 6 punteros más para gestionar la estructura de árbol rojo-negro balanceado.
Dependiendo de la cantidad de memoria con la que estemos ejecutando la JVM, usará punteros de 32 o de 64 bits, por lo que todos los atributos de tipo referencia ocuparán el doble de espacio. La memoria ocupada por una instancia de Node y TreeNode dependiendo del tamaño de los punteros es:
| 32 bits | 64 bits | |
|---|---|---|
| Node | 32 bytes | 48 bytes |
| TreeNode | 56 bytes | 104 bytes |
En mi caso es muy habitual lanzar procesos con más de 32GB de memoria, por lo que me veo obligado a usar direccionamiento de 64 bits, y la diferencia entre la versión de listas enlazadas y la de árbol es de más del doble de memoria.
A todo esto hay que añadir la gestión que hace HashMap del array interno: su tamaño varía en función del número de elementos almacenados en el HashMap, sin ninguna relación sobre cómo esté distribuido su contenido por sus colisiones. Por tanto cuanto más contenido tenga el HashMap, más grande será el array, intentando distribuir todos sus elementos a lo largo del array (infructuosamente si tu función hash es mala).
Si el número de colisiones es muy alto, los elementos se concentrarán en unas pocas posiciones del array, mientras que el resto estarán vacías. Si volvemos a mi ejemplo de 50.000 productos y 1.000 tiendas, un HashMap que contenga su producto cartesiano usando la función hash estándar con direcciones de memoria de 32 bits, nos encontramos con que:
- Existen 49.997.768 instancias de TreeNode que ocupan 2.799.875.008 bytes
- Existen 2.232 instancias de tipo Node que ocupan 71.424 bytes
- El array tiene 67.108.864 posiciones que ocupa 268.435.456 bytes
- 496 de ellas contiene elementos de tipo Node
- 1.550.473 de ellas contiene elementos de tipo TreeNode
- 65.557.895 de ellas están vacías, el 97,69% de las posiciones!!
Tenemos que el mapa ocupa 2,86 GB de memoria, sin contar con el espacio empleado por las instancias que sirven de clave ni el valor asociado. En direccionamiento de 64 bits el mapa ocupa 5,34GB, un 85% más. Esto pone de relieve que casi toda la información del TreeNode son punteros.
Consumo de CPU
Cuando consultas o insertas un valor en un HashMap y se encuentra con una colisión, tiene que recorrer el listado de elementos buscando si alguno de los elementos coincide en su valor de hash y en la identidad de la clave. La forma de determinar si dos claves son idénticas es haciendo uso de la función equals que deberías haber redefinido.
Por tanto en cada operación de acceso, puede llegar a tener que hacer hasta 8 comparaciones en el caso de usar todavía una lista, o Log2(N) en caso de haber pasado a un árbol, siendo N el número medio de elementos en los árboles.
Cambiando a un árbol balanceado, HashMap consigue mantener a raya el coste de encontrar el valor en el hashing abierto, a costa de consumir más memoria.
Si volvemos a los números de mi ejemplo, nos encontramos con que para poder insertar los 50 millones de elementos, se llama 942.272.996 veces al método equals de la clase que hace de clave: unas 19 veces por elemento insertado. Como referencia, en mi ordenador tarda 120 segundos en crear el mapa.
Cuando en Nextail hice profiling de la aplicación, me sorprendió mucho que un gran porcentaje del tiempo de ejecución se empleaba en la función equals. Lo primero que pensé fue que la habíamos implementado mal, dedicando tiempo a entender qué tenía de malo su implementación (la estándar de Java). Hasta que me di cuenta que no había nada malo: sólo que se llamaba demasiadas veces. Este fue el momento clave para entender que teníamos un problema en la función hash asociada.
No tengo el conocimiento suficiente para medirlo y sacar conclusiones, pero seguro que convertir objetos de tipo Node a TreeNode tiene impacto en el recolector de basura, y que objetos de tamaño más grande deben penalizar también el uso de las líneas de caché de la CPU.
La solución
Como dije al principio, el cambio de una sola línea de código puede suponer un cambio radical en el consumo de recursos de tu aplicación. En este caso la línea de código reside en la implementación del método hashCode:
public class MyObjectKey {
public int hashCode() {
return (firstKey << 16) + secondKey;
}
}
¿Cuál es la clave de mi solución? Precisamente el origen del problema: los identificadores de mis objetos son valores que están dentro de un rango bajo de enteros y son valores consecutivos, poco dispersos. Esto hace que los resultados de la función hash acaben concentrados en un rango pequeño de enteros.
La función hash debe devolver un entero de 32 bits, pero los valores que intervienen en su cálculo son enteros que no superan los 16 bits de información, por tanto podemos formar un entero de 32 bits, usando 16 de ellos en la parte más significativa del entero y los otros 16 en la parte menos significativa del entero. De esta forma garantizaremos que la función hash nunca devolverá dos valores que colisionen, minimizando a su vez el número de colisiones dentro del array.
Dependiendo del dominio de la aplicación, si uno de los identificadores toma valores superiores a 65.535, puedes jugar con el número de bits, usando más para un valor y menos para el otro.
Por ejemplo, usando 20 para el identificador de productos y 12 bits para tiendas tendríamos: (firstKey << 12) + secondKey
- 220 = 1.048.576 posibles productos
- 212 = 4.096 posibles tiendas
En el caso de que los dos rangos no fueran suficientemente grandes para los identificadores del dominio empezaríamos a tener colisiones, pero seguirían siendo bastante menos comparado con la función hash por defecto.
Los números
Dada esta función hash, ¿cómo queda el HashMap equivalente? Con los mismos 50.000 productos y 1.000 tiendas, un HashMap que contenga su producto cartesiano usando la nueva función hash con direcciones de memoria de 32 bits tenemos:
- No existe ninguna instancia de tipo TreeNode
- Existen 50.000.000 instancias de tipo Node que ocupan 1.600.000.000 bytes
- El array tiene 67.108.864 posiciones que ocupa 268.435.456 bytes
- 50.000.000 de ellas contiene elementos de tipo Node
- 17.108.864 de ellas están vacías
Por tanto cada instancia de Node está ubicada en una posición distinta del array, y no existen colisiones internas en el array. El tamaño del array es 226, la potencia de dos inmediatamente superior a los 50 millones de registros.
En total estamos consumiendo 1,74 GB de memoria en la versión de 32 bits, mientras que en 64 bits son 2,74 GB.
| 32 bits | 64 bits | |
|---|---|---|
| Optimizado | 1,74GB | 2,74GB |
| Hash estándar | 2,86 GB | 5,34 GB |
| % memoria | +64% | +95% |
Respecto al consumo de CPU, pasa a tardar 80 segundos en crear el mismo HashMap, frente a los 120 de la versión subóptima (un 50% más de tiempo!). El número de llamadas a la función equals de la clave pasa a ser cero. Como la función hash siempre da un resultado distinto no necesita verificar la igualdad de objetos.
Conclusión
La librería de colecciones de Java es uno de los puntos fuertes de la plataforma, ya que nos ayuda a estandarizar el código y nos ahorra el trabajo de tener que construir nuestras librerías de tipos abstractos de datos.
Pero nos lo ha puesto tan fácil que nos ha hecho más vagos (yo incluido) y dejamos de prestar atención a las mismas. No mucha gente conoce la diferencia entre un HashSet y un TreeSet, o qué propiedades tiene un LinkedHashMap frente a un HashMap (son un clásico en las preguntas de entrevistas de trabajo). Para ser productivos, además de la sintaxis de un lenguaje deberíamos dominar las librerías que forman su core.
Sin volvernos locos revisando todo nuestro código (ya sabéis que la optimización prematura es la raíz de todos los males), tened siempre en cuenta la naturaleza de los datos que tengáis por debajo y de las distintas complejidades de los algoritmos. En mi caso entender cómo se aplica el método hashCode en un mapa fue clave para arreglar un problema de rendimiento.
El ejemplo que he utilizado ha sido ilustrativo, y es pesimista al usar el producto cartesiano de productos y tiendas, y además todos los identificadores están en un rango muy compacto de números. En los problemas que resuelvo en el día a día no es así: es un subconjunto de ese producto cartesiano y los identificadores están más dispersos, pero no lo suficiente como para librarme del problema de las colisiones y ser evidente en un análisis de rendimiento.
El ejemplo se podría haber resuelto mejor con una matriz bidimensional, o utilizando otras estructuras de datos que se adaptan mejor a este tipo de problemas. En un próximo post, partiendo del mismo problema, haré un análisis para comparar entre Map<MyObjectKey, MyObject> y Map<Integer, Map<Integer, MyObject>>.
¡Como siempre, cualquier comentario y aportación será bienvenida en los comentarios!